FÓRMULAS DE PRIMER ORDEN DE LA TRIGONOMETRÍA ESFÉRICA

Resolver un triángulo esférico es calcular tres elementos del mismo una vez que se conocen los otros tres. Para ello se empleara las fórmulas fundamentales de la trigonometría esférica. Las de primer orden nos relacionan los ángulos y lados enteros a través de sus funciones trigonométricas. Las de segundo orden relacionan los semielementos de los triángulos esféricos a través de esas mismas funciones.

Fórmulas de Bessel

Para encontrar las relaciones entre lados y ángulos del triángulo esférico se parte de un sistema de coordenadas rectangulares.

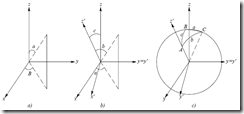
Figura. Deducción de las relaciones entre lados y ángulos

El punto P dista del origen una unidad y tiene coordenadas P = ( x, y, z). Por inspección de la a, se ve que estas coordenadas pueden ser expresadas mediante:

x = sen a • cos b
y = sen a • sen b
z = cos a

Que resulta ser lo mismo que un cambio a coordenadas esféricas.

Si ahora se hace un giro en torno al eje y, de amplitud c figura b, hace que el punto P = (x´, y´, x´) sigua distando una unidad del origen, pero sus coordenadas esféricas son ahora:

x = sen b • cos(180° ‐ A)
y = sen a • sen(180° ‐ A)
z = cos b

Pero, como se hizo una rotación en torno a un eje fijo, las expresiones anteriores están relacionadas mediante una matriz de giro:

Esta expresión matricial proporciona las relaciones entre los ángulos y los lados de un triángulo esférico, pero esto es cierto siempre y cuando la nomenclatura de los ángulos en las figuras (a) y (b) sean consecuentes con un triángulo esférico. Se puede ver que esta nomenclatura coincide con la realidad en la figura (c). Por tanto, se puede realizar operaciones en esa expresión matricial y encontrar unas fórmulas relacionando ángulos y lados del triángulo esférico:

cos a = cos b • cos c + sen a • sen b • cos A                  Primera formula de Bessel
sen a • sen B = sen b • sen A                                             Segunda formula de Bessel
sen a • cos B = cos b • sen c – sen b • cos c • cos A     Tercera formula de Bessel

Estas tres fórmulas son totalmente generales y se pueden obtener para otros ángulos mediante permutaciones cíclicas de los ángulos. La primera fórmula de Bessel también recibe el nombre de teorema del coseno. La segunda fórmula de Bessel se conoce como teorema del seno.

Fórmula de la cotangente

Esta fórmula se obtiene dividiendo la ecuación por la (en el término a la izquierda del signo igual se divide por sen a • sen B mientras que el término a la derecha se divide por sen b • sen A):