Exceso Esférico de un Triángulo

Se llama exceso esférico de un triangulo, el valor en que la suma de sus tres ángulos excede de dos rectos,

ε = A + B + C −180º

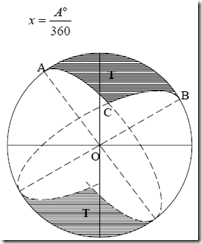
Sea el triangulo ABC limitado por tres círculos máximos. Suponiendo que el lado AB coincide con el plano de la figura. Cada vértice del triangulo, produce en la esfera un sector de superficie conocida. En efecto, considerando como 1 al área de la esfera y A° es el valor en grados de dicho huso, se escribe:

360º ‐‐‐‐‐‐‐‐‐‐‐‐‐‐ 1
Aº ‐‐‐‐‐‐‐‐‐‐‐‐‐‐ x

de donde,

Figura Triangulo esférico

Por otra parte, sumando las áreas de los tres sectores de ángulos A, B, C resulta contando dos veces el triangulo cuya superficie se denomina T, es decir

El sumando 1/2 corresponde a la media esfera exterior al papel. Por otra parte, escribiendo el área del triangulo como parte del área de la esfera, cuyo valor es

4π R2

se tiene

y de aquí

de donde

al suprimir el 360° con el 2π, lo que resta es el exceso esférico en radianes, o escrito en segundos

Este valor es utilizado en el caso de triángulos esféricos y también de triángulos elipsóidicos, cuyos lados sean pequeños frente al radio de la esfera. Muchas veces no habrá error en considerar

Se hará una mayor aplicación en el tema de curvas alabeadas del concepto de exceso esférico a los triángulos que constituyen las redes geodésicas de los distintos órdenes.