La descripción probabilística del flujo vehicular considera los siguientes aspectos de su comportamiento:
- Los vehículos circulan en grupos con un intervalo promedio de cada uno
- Los vehículos circulan en forma completamente dispersa
- El patrón de llegadas o paso de vehículos corresponde a un proceso aleatorio
La distribución de probabilidades de Poisson formula los siguientes supuestos para su aplicación:
- Cada conductor sitúa su vehículo independientemente de los demás, excepto cuando su espaciamiento es muy pequeño
- El número de vehículos que pasan por un punto en un intervalo de tiempo dado es independiente del número de vehículos que pasan por otro punto durante el mismo intervalo.
- El número de vehículos que pasan por un punto dado en un intervalo de tiempo es independiente del número de vehículos que pasan por el mismo punto durante otro intervalo.
Siguiendo la distribución de llegadas de tipo Poisson, la probabilidad de x llegadas en un intervalo de tiempo t se calcula con la siguiente fórmula:
Donde:
X = Variable aleatoria que representa el número de llegadas de vehículos a un punto
p(x) = Probabilidad que lleguen exactamente x vehículos al punto durante el intervalo de tiempo t
m = Número promedio de vehículos que se espera lleguen durante el intervalo de tiempo t (vehículos / intervalo)
e = Base de los logaritmos neperianos
Si se calcula la probabilidad de que no lleguen vehículos en el intervalo de tiempo t se tiene (para t ≥ 0):
Al no llegar ningún vehículo, entonces se tiene un intervalo h mayor o igual que t, entonces se puede formular las siguientes expresiones (para t, t1, t2 ≥ 0):
Se puede calcular también las siguientes probabilidades acumulativas:
-Probabilidad de que lleguen N o menos vehículos
-Probabilidad de que lleguen más de N vehículos
-Probabilidad de que lleguen menos de N vehículos
-Probabilidad de que lleguen N o más vehículos

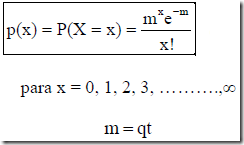






0 comentarios::
Publicar un comentario