Máximos absolutos para fuerza Cortante y momento Flexionante

En la determinación de las líneas de influencia uno de los problemas de mayor importancia es el de la determinación tanto de la posición del punto en la viga, como de la posición de la carga sobre la viga, de manera que se pueda obtener los máximos absolutos tanto de la fuerza cortante y el momento flexionante, causados por las cargas móviles. Si la viga es en voladizo o simplemente apoyada, este problema puede resolverse fácilmente.

Fuerza cortante.

Para una viga en voladizo, la fuerza cortante máxima absoluta ocurrirá en un punto localizado justamente al lado del empotramiento. La fuerza cortante máxima se encuentra por el método de las secciones, con las cargas situadas cerca del soporte, la primera situada justa­mente al lado de la sección, como se muestra en la figura.

En vigas simplemente apoyadas, la fuerza cortante máxima absoluta ocurrirá justamente al lado de uno de los soportes. En este caso las cargas se sitúan de manera que la primera en secuencia se coloque cerca del soporte, como se muestra en la figura.

Momento flexionante.

El momento máximo absoluto para una viga en voladizo ocurre en el mismo punto en que ocurre la fuerza cortante máxima absoluta, aun­que en este caso, las cargas concentradas deben situarse en el extremo alejado de la viga, como en la figura.

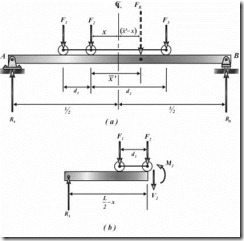
Para una viga simplemente apoyada, las posiciones críticas de las cargas y el momento máximo absoluto asociado, no pueden en gene­ral, determinarse por simple inspección. Sin embargo se puede determinar analíticamente estas posiciones. Para fines de análisis, se considerará una viga simplemente apoyada, sometida a la acción de fuerzas F₁, F₂ y F₃, que se muestran en la figura a.

Como el diagrama de momentos para una serie de fuerzas concentra­das consiste en segmentos de líneas rectas con puntos máximos en cada fuerza, entonces el momento máximo absoluto ocurrirá bajo alguna de estas fuerzas. Supongamos que este momento máximo ocurre bajo la carga F₂. La posición de las cargas F₁, F₂ y F₃ sobre la viga estará claramente especificada por la distancia x, medida desde F₂ al centro del claro de la viga, como se muestra en la figura a.

Para determinar un valor específico de x, obtenemos prime­ro la fuerza resultante del sistema, F_R y su distancia , medida desde F₂. Una vez hecho esto, sumamos los momentos respecto a B, lo que da la reacción izquierda de la viga R_A, esto es;

Si se toma la sección de la viga entre el apoyo A y la carga F₂ , el diagrama de cuerpo libre resultante es el que se muestra en la figura b. Entonces el momento M₂ bajo la carga F₂ será;

por lo tanto tenemos;

  ó  

Por lo tanto, podemos concluir que el momento máximo absoluto en una viga simplemente apoyada ocurre bajo una de las fuerzas concentradas cuando esta fuerza se coloca sobre la viga de manera que ella y la fuerza resultante del sistema estén equidistantes del centro de la viga. Como se tiene una serie de cargas sobre el claro de la viga (por ejemplo, F₁, F₂ , F₃, en la figura a este principio tendrá que aplicarse a cada carga de la serie y calcularse el momento máximo correspondiente.

Por compa­ración, el momento máximo será el máximo absoluto. Como regla general, el momento máximo absoluto ocurre con frecuencia bajo la fuerza más grande que se encuentre más cercana a la fuerza resultan­te del sistema.

Envolvente de valores máximos de líneas de influencia.

Es difícil establecer reglas o fórmulas para determinar las fuerzas cor­tantes o momentos flexionantes máximos absolutos para vigas sopor­tadas de manera distinta a las vistas aquí hasta ahora, esto es, simple­mente apoyado o en voladizo. Sin embargo, una manera elemental de resolver este problema requiere construir líneas de influencia para la fuerza cortante o el momento en puntos seleccionados a lo largo de la longitud entera de la viga, y luego calcular la fuerza cortante o momento máximos en la viga para cada punto usando algunos de los métodos estudiados y aprendidos en las materias correspondientes. Esos valores dan una "envolvente de máximos" cuan­do se grafican; de aquí pueden encontrarse los valores máximos abso­lutos para la fuerza cortante y el momento, así como su localización.

Obviamente, es deseable una solución por computadora para este problema, ya que el trabajo puede ser bastante tedioso si se efectúa a mano.

A continuación se explicará una metodología que facilitara de gran manera la construcción de las líneas de influencia.